36  分类问题

library(nnet)     # 多项回归/神经网络 multinom / nnet
library(MASS)     # 线性/二次判别分析 lda / qda
library(glmnet)   # 惩罚多项回归 glmnet
library(e1071)    # 朴素贝叶斯 naiveBayes 和支持向量机 svm
library(kernlab)  # 支持向量机分类 ksvm
library(class)    # K 最近邻 knn
library(rpart)    # 决策树分类 rpart
library(randomForest) # 随机森林 randomForest
# library(gbm)        # 梯度提升机
library(xgboost)      # 集成学习
library(lattice)

以 iris 数据集为例，简单，方便介绍模型和算法，定位入门。分类间隔最大化，也是一个优化问题，找一条分界线，一个分割面，一个超平面划分不同的种类。本章篇幅：每个算法 4 页，共计 40 页。10 个算法的介绍按照分类思路，模型，代码和参数说明，分类性能评估。应用案例是手写数字识别。要点不是数据如何复杂，而是怎样把理论写得通俗、准确，看了之后能够应用到复杂的真实数据分析场景中去。理论解释、绘图说明、经验总结。

1. 线性分类器
   2. 多项回归模型
   3. 线性判别分析
2. 非线性分类器
   1. 二次判别分析
   2. 朴素贝叶斯
   3. 支持向量机
   4. K 最近邻
   5. 神经网络
   6. 决策树
   7. 随机森林
   8. 集成学习

iris 数据集也来自 Base R 自带的 datasets 包，由 Anderson Edgar 收集，最早见于 1935 年的文章，后被 Ronald Fisher 在研究分类问题时引用 (Fisher 1936)。到如今，在机器学习的社区里，提及 iris 数据集，一般只知 Fisher 不知 Anderson。

提示

1. 鸢尾花数据集，逻辑回归拟合，绘制分类边界图，实现 R 版本。
2. 参考文献《机器学习的概率视角导论》 (Murphy 2022) 书中图 2.13 的 Python 代码
3. 将回归模型用 SQL 表达出来，放在数据库上高性能地执行分类预测。

36.1 多项回归模型

library(nnet) # 多项逻辑回归
iris_multinom <- multinom(Species ~ ., data = iris, trace = FALSE)
summary(iris_multinom)

Call:
multinom(formula = Species ~ ., data = iris, trace = FALSE)

Coefficients:
           (Intercept) Sepal.Length Sepal.Width Petal.Length Petal.Width
versicolor    18.69037    -5.458424   -8.707401     14.24477   -3.097684
virginica    -23.83628    -7.923634  -15.370769     23.65978   15.135301

Std. Errors:
           (Intercept) Sepal.Length Sepal.Width Petal.Length Petal.Width
versicolor    34.97116     89.89215    157.0415     60.19170    45.48852
virginica     35.76649     89.91153    157.1196     60.46753    45.93406

Residual Deviance: 11.89973 
AIC: 31.89973 

table(predict(iris_multinom, iris[, -5], type = "class"), iris[, 5])

            
             setosa versicolor virginica
  setosa         50          0         0
  versicolor      0         49         1
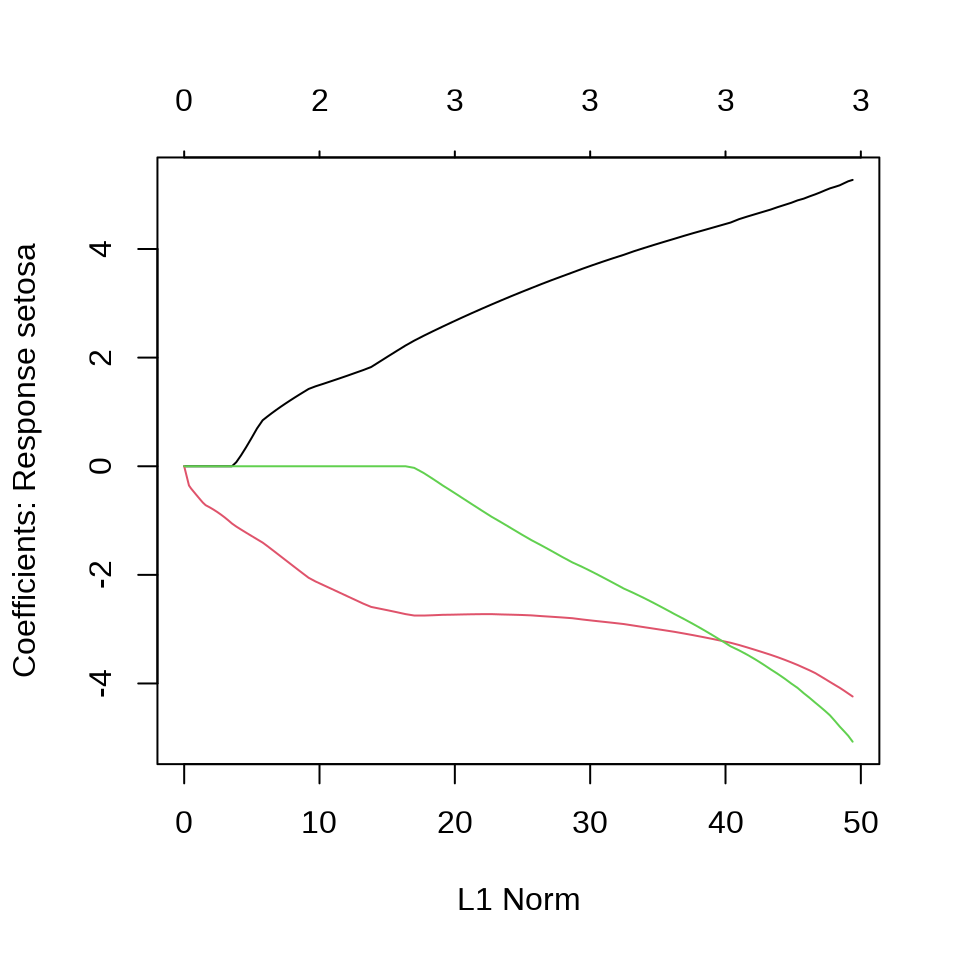
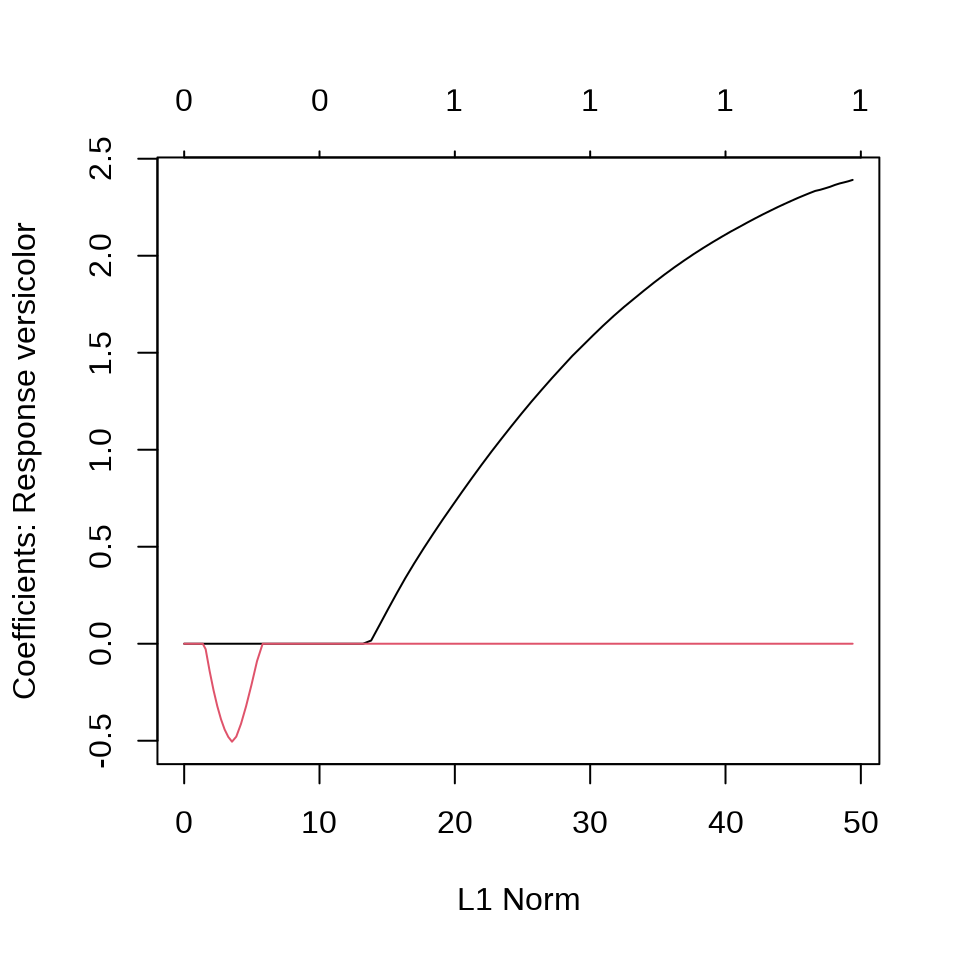
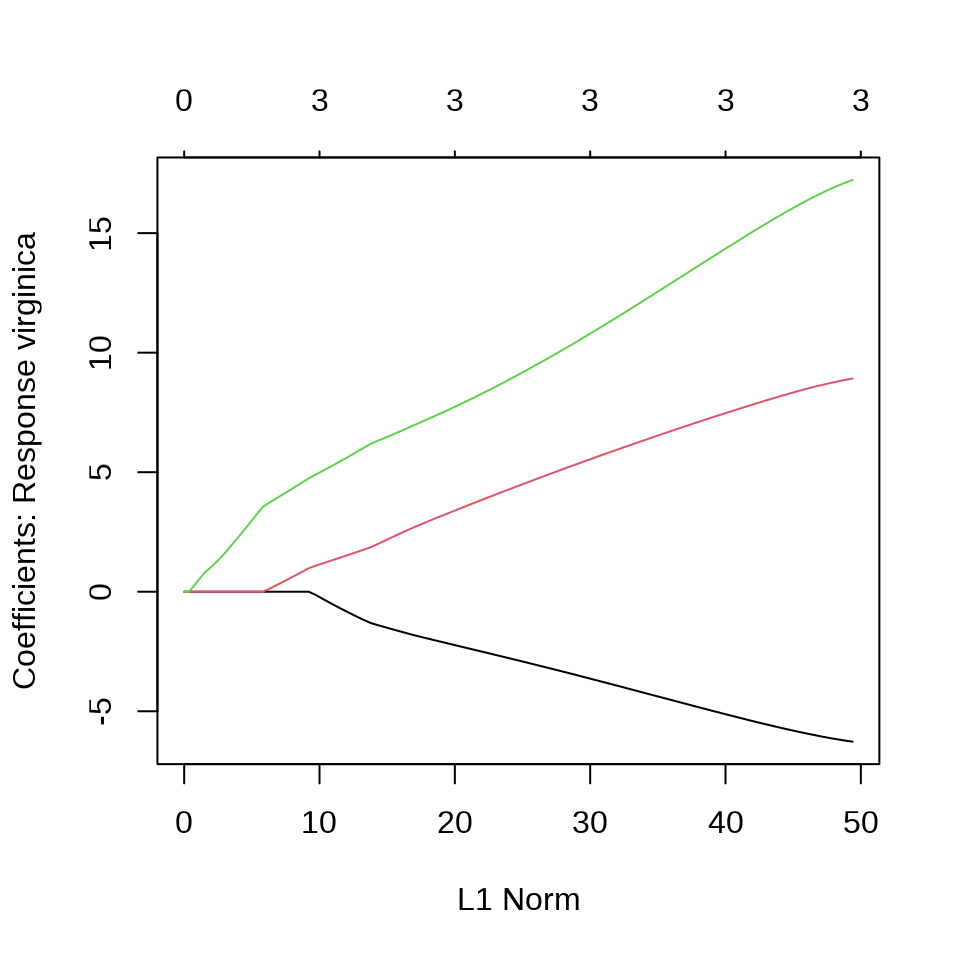
  virginica       0          1        49

在有的数据中，观测变量之间存在共线性，采用变量选择方法，比如 Lasso 方法压缩掉一部分变量。

library(glmnet) # 多项回归
iris_glmnet <- glmnet(x = iris[, -5], y = iris[, 5], family = "multinomial")

plot(iris_glmnet)

图 36.1: 回归系数的迭代路径

图 36.2: 回归系数的迭代路径

图 36.3: 回归系数的迭代路径

plot(iris_glmnet$lambda,
  ylab = expression(lambda), xlab = "迭代次数",
  main = "惩罚系数的迭代路径"
)

图 36.4: 惩罚系数的迭代路径

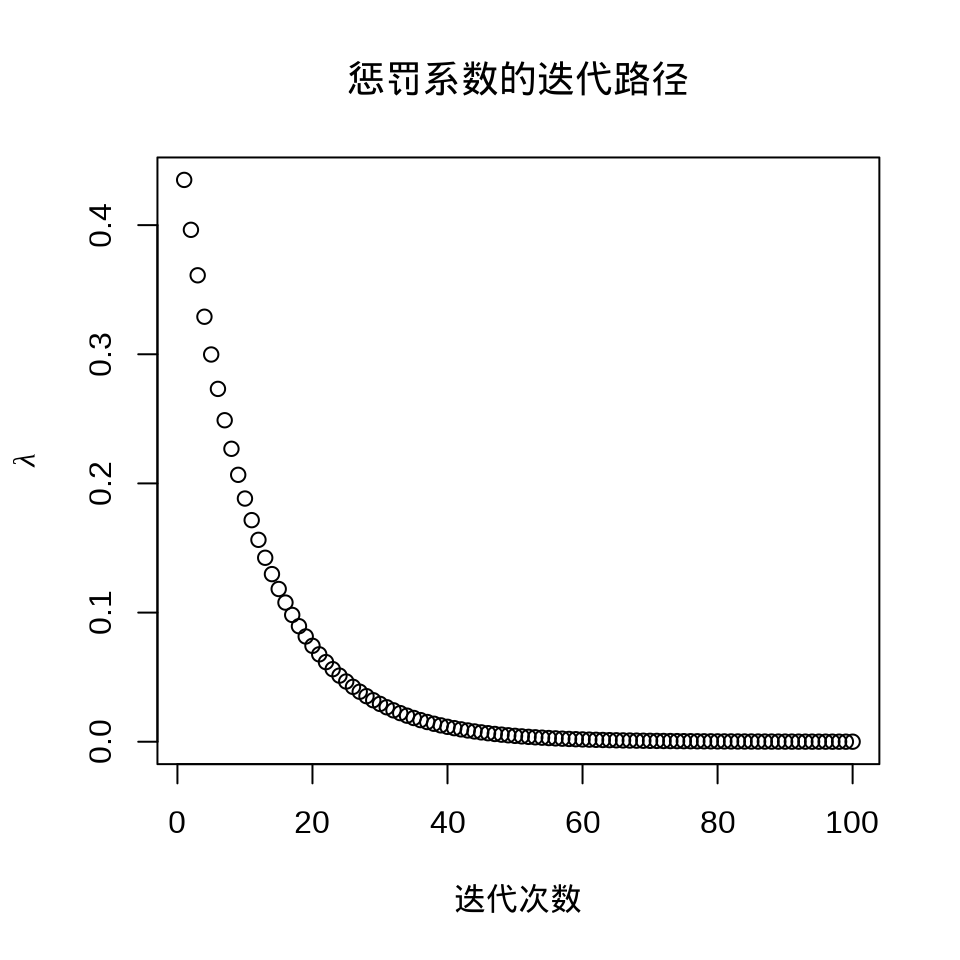
选择一个迭代趋于稳定时的 lambda，比如 iris_glmnet$lambda[80] 。

coef(iris_glmnet, s = 0.0002796185)

$setosa
5 x 1 sparse Matrix of class "dgCMatrix"
                     1
(Intercept)  17.015429
Sepal.Length  .       
Sepal.Width   4.486992
Petal.Length -3.250342
Petal.Width  -3.315393

$versicolor
5 x 1 sparse Matrix of class "dgCMatrix"
                    1
(Intercept)  8.132656
Sepal.Length 2.123980
Sepal.Width  .       
Petal.Length .       
Petal.Width  .       

$virginica
5 x 1 sparse Matrix of class "dgCMatrix"
                      1
(Intercept)  -25.148085
Sepal.Length   .       
Sepal.Width   -5.176029
Petal.Length   7.536940
Petal.Width   14.481524

iris_pred_glmnet <- predict(
  object = iris_glmnet, newx = as.matrix(iris[, -5]),
  s = 0.0002796185, type = "class"
)

table(iris_pred_glmnet, iris[, 5])

                
iris_pred_glmnet setosa versicolor virginica
      setosa         50          0         0
      versicolor      0         49         1
      virginica       0          1        49

36.2 线性判别分析

library(MASS)
# lda
iris_lda <- lda(Species ~ ., data=iris)
iris_lda

Call:
lda(Species ~ ., data = iris)

Prior probabilities of groups:
    setosa versicolor  virginica 
 0.3333333  0.3333333  0.3333333 

Group means:
           Sepal.Length Sepal.Width Petal.Length Petal.Width
setosa            5.006       3.428        1.462       0.246
versicolor        5.936       2.770        4.260       1.326
virginica         6.588       2.974        5.552       2.026

Coefficients of linear discriminants:
                    LD1         LD2
Sepal.Length  0.8293776 -0.02410215
Sepal.Width   1.5344731 -2.16452123
Petal.Length -2.2012117  0.93192121
Petal.Width  -2.8104603 -2.83918785

Proportion of trace:
   LD1    LD2 
0.9912 0.0088 

# 预测
iris_lda_pred <- predict(iris_lda, iris[, -5])$class

# 预测结果
table(iris_lda_pred, iris[, 5])

             
iris_lda_pred setosa versicolor virginica
   setosa         50          0         0
   versicolor      0         48         1
   virginica       0          2        49

36.3 二次判别分析

# Quadratic Discriminant Analysis 二次判别分析
iris_qda <- qda(Species ~ ., data=iris)
iris_qda

Call:
qda(Species ~ ., data = iris)

Prior probabilities of groups:
    setosa versicolor  virginica 
 0.3333333  0.3333333  0.3333333 

Group means:
           Sepal.Length Sepal.Width Petal.Length Petal.Width
setosa            5.006       3.428        1.462       0.246
versicolor        5.936       2.770        4.260       1.326
virginica         6.588       2.974        5.552       2.026

# 预测
iris_qda_pred <- predict(iris_qda, iris[, -5])$class

# 预测结果
table(iris_qda_pred, iris[, 5])

             
iris_qda_pred setosa versicolor virginica
   setosa         50          0         0
   versicolor      0         48         1
   virginica       0          2        49

代码

library(mda)
# Mixture Discriminant Analysis 混合判别分析
iris_mda <- mda(Species ~ ., data = iris)
# 预测
iris_mda_pred <- predict(iris_mda, newdata = iris[, -5])
# 预测结果
table(iris_mda_pred, iris[, 5])

# Flexible Discriminant Analysis 灵活判别分析
iris_fda <- fda(Species ~ ., data = iris)
# 预测
iris_fda_pred <- predict(iris_fda, newdata = iris[, -5])
# 预测结果
table(iris_fda_pred, iris[, 5])

# Regularized Discriminant Analysis 正则判别分析
library(klaR)
iris_rda <- rda(Species ~ ., data = iris, gamma = 0.05, lambda = 0.01)
# 输出结果
summary(iris_rda)
# 预测
iris_rda_pred <- predict(iris_rda, newdata = iris[, -5])$class
# 预测结果
table(iris_rda_pred, iris[, 5])

36.4 朴素贝叶斯

library(e1071) # 朴素贝叶斯
iris_nb <- naiveBayes(Species ~ ., data = iris)
iris_nb

Naive Bayes Classifier for Discrete Predictors

Call:
naiveBayes.default(x = X, y = Y, laplace = laplace)

A-priori probabilities:
Y
    setosa versicolor  virginica 
 0.3333333  0.3333333  0.3333333 

Conditional probabilities:
            Sepal.Length
Y             [,1]      [,2]
  setosa     5.006 0.3524897
  versicolor 5.936 0.5161711
  virginica  6.588 0.6358796

            Sepal.Width
Y             [,1]      [,2]
  setosa     3.428 0.3790644
  versicolor 2.770 0.3137983
  virginica  2.974 0.3224966

            Petal.Length
Y             [,1]      [,2]
  setosa     1.462 0.1736640
  versicolor 4.260 0.4699110
  virginica  5.552 0.5518947

            Petal.Width
Y             [,1]      [,2]
  setosa     0.246 0.1053856
  versicolor 1.326 0.1977527
  virginica  2.026 0.2746501

# 预测
iris_nb_pred <- predict(iris_nb, newdata = iris, type = "class")
# 预测结果
table(iris_nb_pred, iris[, 5])

            
iris_nb_pred setosa versicolor virginica
  setosa         50          0         0
  versicolor      0         47         3
  virginica       0          3        47

36.5 支持向量机

e1071 包也提供支持向量机

# e1071
iris_svm <- svm(Species ~ ., data = iris)
iris_svm

Call:
svm(formula = Species ~ ., data = iris)


Parameters:
   SVM-Type:  C-classification 
 SVM-Kernel:  radial 
       cost:  1 

Number of Support Vectors:  51

# 预测
iris_svm_pred <- predict(iris_svm, newdata = iris, probability = FALSE)
# 预测结果
table(iris_svm_pred, iris[, 5])

             
iris_svm_pred setosa versicolor virginica
   setosa         50          0         0
   versicolor      0         48         2
   virginica       0          2        48

kernlab 包提供核支持向量机。

library(kernlab)
iris_ksvm <- ksvm(Species ~ ., data = iris)
iris_ksvm

Support Vector Machine object of class "ksvm" 

SV type: C-svc  (classification) 
 parameter : cost C = 1 

Gaussian Radial Basis kernel function. 
 Hyperparameter : sigma =  0.661791902353537 

Number of Support Vectors : 59 

Objective Function Value : -4.1441 -4.5174 -20.779 
Training error : 0.026667 

kernlab 包 (Karatzoglou 等 2004) 的绘图函数 plot() 仅支持二分类模型。

iris_pred_svm <- predict(iris_ksvm, iris[, -5], type = "response")
table(iris_pred_svm, iris[, 5])

             
iris_pred_svm setosa versicolor virginica
   setosa         50          0         0
   versicolor      0         48         2
   virginica       0          2        48

36.6 K 最近邻

# 将 iris3 数据集拆分为训练集和测试集
iris_train <- rbind(iris3[1:25, , 1], iris3[1:25, , 2], iris3[1:25, , 3])
iris_test <- rbind(iris3[26:50, , 1], iris3[26:50, , 2], iris3[26:50, , 3])
iris_species <- factor(rep(c("setosa", "versicolor", "virginica"), each = 25))

library(class)
# 分 3 类
iris_knn <- knn(
  train = iris_train, test = iris_test,
  cl = iris_species, k = 3, prob = TRUE
)
# 分类结果汇总
table(iris_knn, iris_species) 

            iris_species
iris_knn     setosa versicolor virginica
  setosa         25          0         0
  versicolor      0         23         4
  virginica       0          2        21

36.7 神经网络

library(nnet)
iris_nnet <- nnet(Species ~ ., data = iris, size = 4, trace = FALSE)
summary(iris_nnet)

a 4-4-3 network with 35 weights
options were - softmax modelling 
  b->h1  i1->h1  i2->h1  i3->h1  i4->h1 
  -3.57   -6.33  -13.68   22.78   12.33 
  b->h2  i1->h2  i2->h2  i3->h2  i4->h2 
   1.38    8.97    4.90    6.90    2.63 
  b->h3  i1->h3  i2->h3  i3->h3  i4->h3 
  -2.50  -11.42   -6.36   -5.40   -2.18 
  b->h4  i1->h4  i2->h4  i3->h4  i4->h4 
1508.96  111.92  133.00 -427.16 -304.64 
  b->o1  h1->o1  h2->o1  h3->o1  h4->o1 
  89.58 -324.42   89.40    1.12  114.75 
  b->o2  h1->o2  h2->o2  h3->o2  h4->o2 
-110.27  293.74 -113.18   -2.22  410.77 
  b->o3  h1->o3  h2->o3  h3->o3  h4->o3 
  20.31   29.97   23.91    0.43 -525.84 

size 隐藏层中的神经元数量

iris_pred_nnet <- predict(iris_nnet, newdata = iris[,-5], type = "class")
table(iris_pred_nnet, iris[, 5])

              
iris_pred_nnet setosa versicolor virginica
    setosa         50          0         0
    versicolor      0         49         0
    virginica       0          1        50

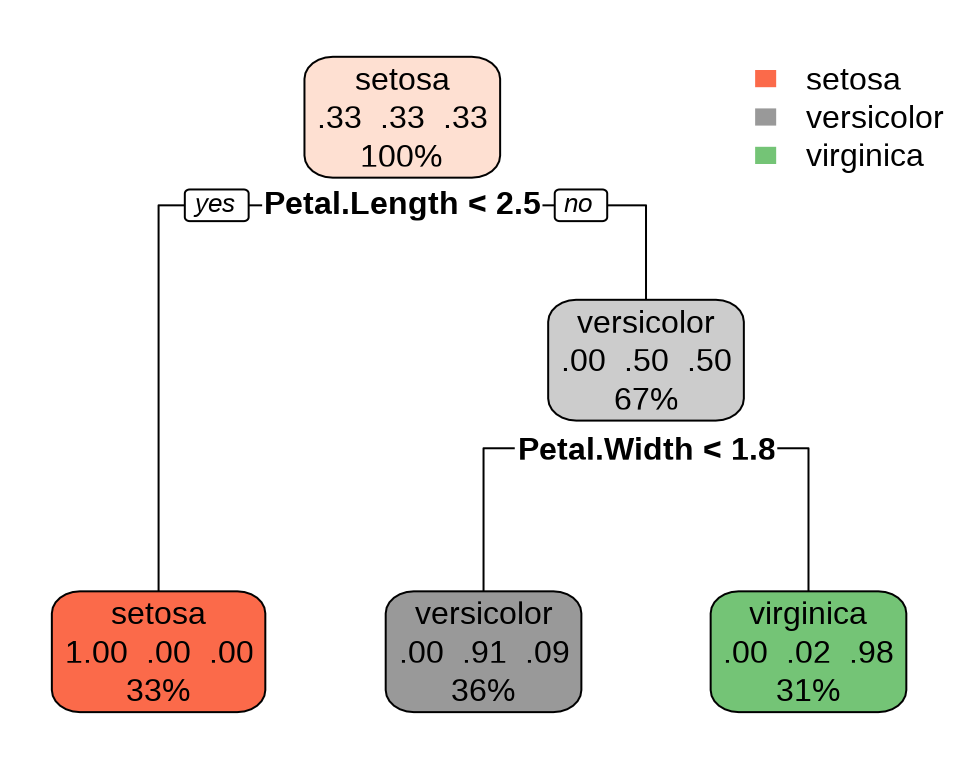
36.8 决策树

library(rpart)
iris_rpart <- rpart(Species ~ ., data = iris)
iris_rpart

n= 150 

node), split, n, loss, yval, (yprob)
      * denotes terminal node

1) root 150 100 setosa (0.33333333 0.33333333 0.33333333)  
  2) Petal.Length< 2.45 50   0 setosa (1.00000000 0.00000000 0.00000000) *
  3) Petal.Length>=2.45 100  50 versicolor (0.00000000 0.50000000 0.50000000)  
    6) Petal.Width< 1.75 54   5 versicolor (0.00000000 0.90740741 0.09259259) *
    7) Petal.Width>=1.75 46   1 virginica (0.00000000 0.02173913 0.97826087) *

library(rpart.plot)
rpart.plot(iris_rpart)

图 36.5: 分类回归树

预测结果，训练误差

# 预测
iris_pred_rpart <- predict(iris_rpart, iris[, -5], type = "class")
# 预测结果
table(iris_pred_rpart, iris[, 5])

               
iris_pred_rpart setosa versicolor virginica
     setosa         50          0         0
     versicolor      0         49         5
     virginica       0          1        45

party 包和 partykit 包也提供类似的功能，前者是基于 C 语言实现，后者基于 R 语言实现。

代码

# 与 rpart 包分类的结果一样
library(partykit)
iris_party <- ctree(Species ~ ., data = iris)
plot(iris_party)
iris_pred_party <- predict(iris_party, iris[, -5], type = "response")
table(iris_pred_party, iris[, 5])

# PART 算法
library(RWeka)
iris_weka <- PART(Species ~ ., data = iris)
# 输出拟合结果
summary(iris_weka)
# 预测
iris_pred_weka <- predict(iris_weka, newdata = iris[, -5], type = "class")
# 预测结果
table(iris_pred_weka, iris[, 5])

# Bagging CART
library(ipred)
iris_ipred <- bagging(Species ~ ., data = iris)
# 输出拟合结果
# summary(iris_ipred)
# 预测
iris_pred_ipred <- predict(iris_ipred, newdata = iris[, -5], type = "class")
# 预测结果
table(iris_pred_ipred, iris[, 5])

# Boosted C5.0
library(C50)
iris_C50 <- C5.0(Species ~ ., data = iris)
# 预测
iris_pred_C50 <- predict(iris_C50, newdata = iris[, -5])
# 预测结果
table(iris_pred_C50, iris[, 5])

# Gradient Boosted Machine
# Warning message:
# Setting `distribution = "multinomial"` is ill-advised 
# as it is currently broken. 
# It exists only for backwards compatibility. Use at your own risk. 
library(gbm)
iris_gbm <- gbm(Species ~ ., data = iris, distribution = "multinomial")
# 预测
iris_pred_gbm <- predict(iris_gbm, newdata = iris[, -5], n.trees = 1, type = "response")
# 转化为与响应变量一样的取值
pred_gbm <- colnames(iris_pred_gbm)[apply(iris_pred_gbm, 1, which.max)]
# 预测结果
table(pred_gbm, iris[, 5])

36.9 随机森林

library(randomForest) # 随机森林
iris_rf <- randomForest(
  Species ~ ., data = iris,
  importance = TRUE, proximity = TRUE
)
# 分类结果
print(iris_rf)

Call:
 randomForest(formula = Species ~ ., data = iris, importance = TRUE,      proximity = TRUE) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 2

        OOB estimate of  error rate: 4%
Confusion matrix:
           setosa versicolor virginica class.error
setosa         50          0         0        0.00
versicolor      0         47         3        0.06
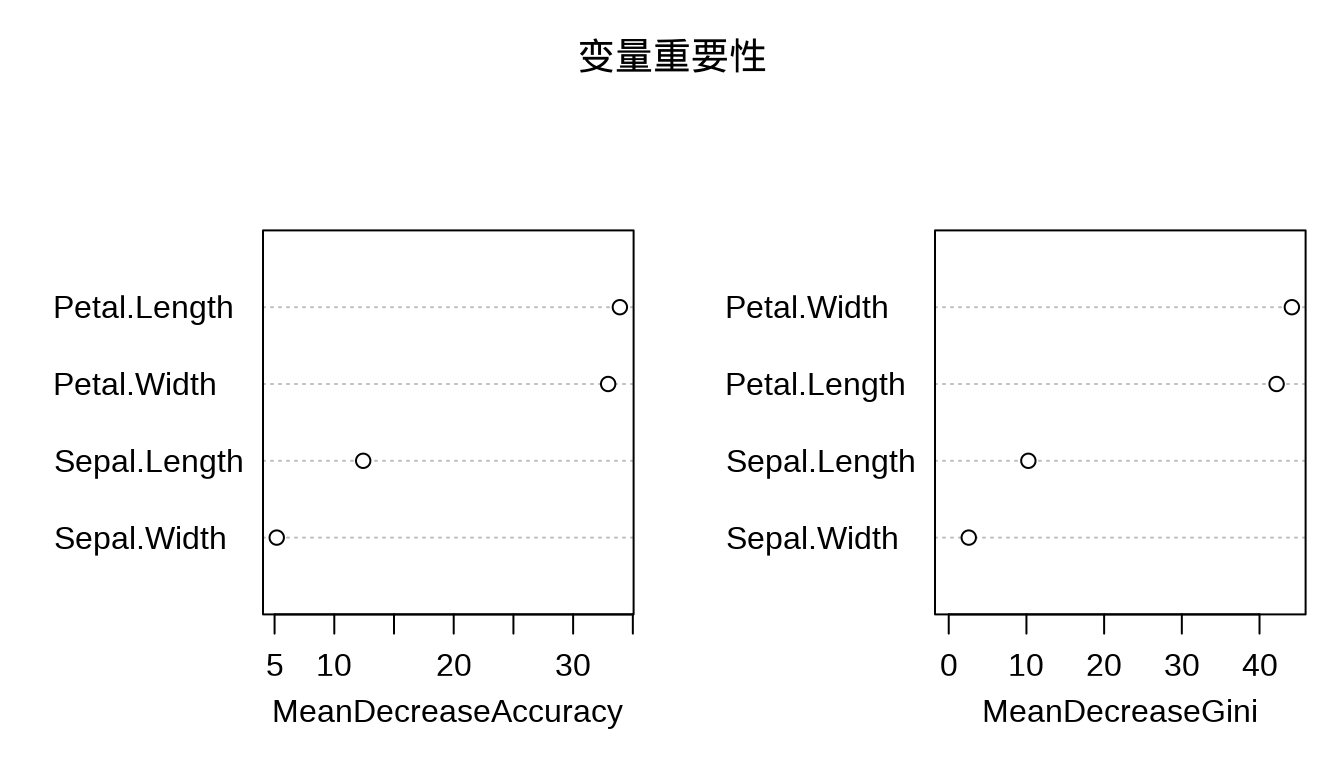
virginica       0          3        47        0.06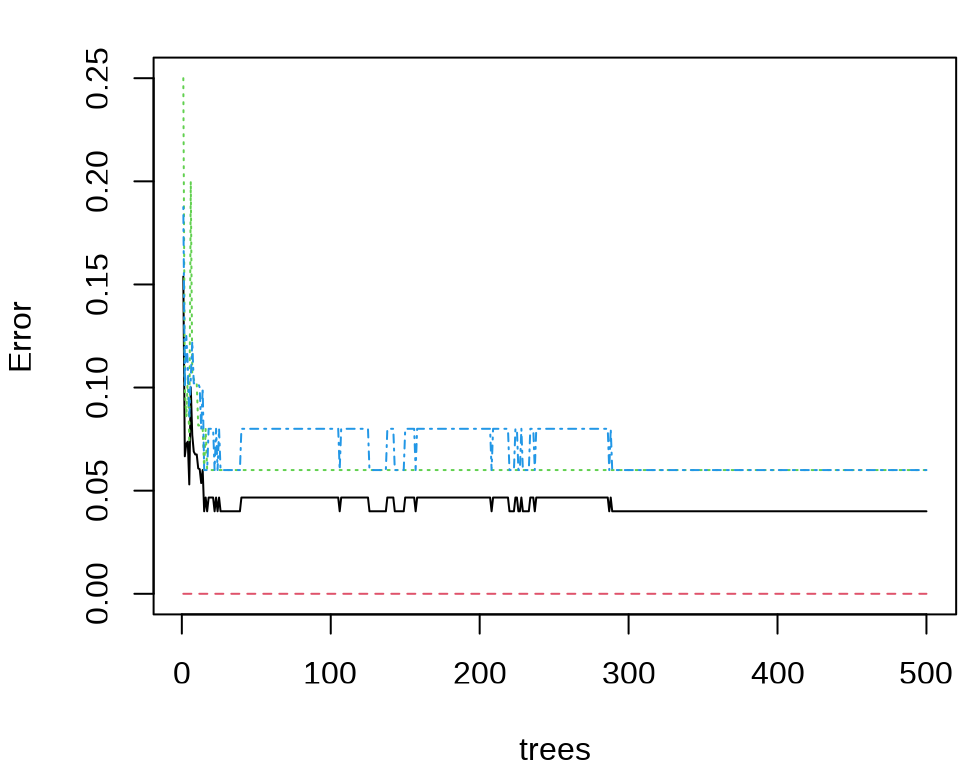

代码

op <- par(mar = c(4, 4, 1.5, 0.1))
plot(iris_rf, main = "")
on.exit(par(op), add = TRUE)

图 36.6: 随机森林

varImpPlot(iris_rf, main = "变量重要性")

图 36.7: 变量重要性

iris_pred_rf <- predict(iris_rf, iris[, -5], type = "response")
table(iris_pred_rf, iris[, 5])

            
iris_pred_rf setosa versicolor virginica
  setosa         50          0         0
  versicolor      0         50         0
  virginica       0          0        50

36.10 集成学习

在训练模型之前，需要先对数据集做预处理，包括分组采样、类别编码、数据拆分、类型转换等。

制作一个函数对数据集添加新列 mark 作为训练集 train 和测试集 test 的采样标记，返回数据。

# 输入数据 x 和采样比例 prop
add_mark <- function(x = iris, prop = 0.7) {
  idx <- sample(x = nrow(x), size = floor(nrow(x) * prop))
  rbind(
    cbind(x[idx, ], mark = "train"),
    cbind(x[-idx, ], mark = "test")
  )
}

为了使采样结果可重复，设置随机数种子，然后对 iris 数据集按列 Species 分组添加采样标记，分组随机抽取 70% 的样本作为训练数据，余下的作为测试数据。就 iris 数据集来说，训练集有 35*3 = 105 条记录，测试集有 15*3 = 45 条记录。

set.seed(20232023)
iris_df <- do.call(rbind, lapply(split(iris, iris$Species), add_mark, prop = 0.7))

为了使用函数 fcase() 对分类变量 Species 做重编码操作，加载 data.table 包，将数据集 iris_df 转为 data.table 类型。值得注意，xgboost 包要求分类变量的类别序号必须从 0 开始。

# 数据准备
library(data.table)
iris_dt <- as.data.table(iris_df)
iris_dt <- iris_dt[, Species := fcase(
  Species == "setosa", 0,
  Species == "versicolor", 1,
  Species == "virginica", 2
)]

将数据 iris_dt 拆分成训练集和测试集，并以列表结构存储数据，样本数据及标签以矩阵类型存储。

# 训练数据
iris_train <- list(
  data = as.matrix(iris_dt[iris_dt$mark == "train", -c("mark", "Species")]),
  label = as.matrix(iris_dt[iris_dt$mark == "train", "Species"])
)
# 测试数据
iris_test <- list(
  data = as.matrix(iris_dt[iris_dt$mark == "test", -c("mark", "Species")]),
  label = as.matrix(iris_dt[iris_dt$mark == "test", "Species"])
)

数据准备好后，加载 xgboost 包，设置训练参数，开始训练分类模型。此分类任务中类别超过 2，是多分类任务，学习任务是分类，目标函数可以是 objective = "multi:softprob" 或者 objective = "multi:softmax"，相应的评估指标可以是 eval_metric = "mlogloss" 或者 eval_metric = "merror"。iris 数据集的分类变量 Species 共有 3 类，所以 num_class = 3 。

library(xgboost)
iris_xgb <- xgboost(
  data = iris_train$data, 
  label = iris_train$label,
  objective = "multi:softmax",  # 学习任务
  eval_metric = "mlogloss",     # 评估指标
  nrounds = 2,   # 提升迭代的最大次数
  num_class = 3  # 分类数
)

[1] train-mlogloss:0.747373 
[2] train-mlogloss:0.540389 

将训练好的模型放在测试集数据上进行预测。

# ?predict.xgb.Booster
iris_pred <- predict(object = iris_xgb, newdata = iris_test$data)

将预测结果与测试集中的样本标签对比，检查分类效果。

table(iris_test$label, iris_pred)

   iris_pred
     0  1  2
  0 15  0  0
  1  0 14  1
  2  0  2 13

36.11 总结

不同的分类算法分布在不同的 R 包中，在使用方式上既有相通之处，又有不同之处。下表对多个 R 包的使用做了归纳。R 包之间的不一致性，计算预测分类的概率的语法。

函数	R 包	代码
lda()	MASS	predict(obj)
glm()	stats	predict(obj, type = "response")
gbm()	gbm	predict(obj, type = "response", n.trees)
naiveBayes()	e1071	predict(obj, type = "class")
svm()	e1071	predict(obj, probability = FALSE)
ksvm()	kernlab	predict(obj, type = "response")
mda()	mda	predict(obj, type = "posterior")
rpart()	rpart	predict(obj, type = "prob")
Weka()	RWeka	predict(obj, type = "probability")
ctree()	partykit	predict(obj, type = "response")
bagging()	ipred	predict(obj, type = "class")

36.12 习题

1. titanic 包整理了来自 kaggle 的 Titanic 数据集，详细记录了 891 位乘客的信息，它比 Base R 内置的 Titanic 数据集更加原始，细节更多，信息更加丰富。原数据集拆分为训练集 titanic_train 和测试集 titanic_test。因为有每个乘客的原始信息，我们可以在个体水平上建模，采用更加复杂的模型分析泰坦尼克号乘客存活率及其影响因素。

Fisher, R. A. 1936. 《The Use Of Multiple Measurements In Taxonomic Problems》. Annals of Eugenics 7 (2): 179–88. https://doi.org/10.1111/j.1469-1809.1936.tb02137.x.

Karatzoglou, Alexandros, Alex Smola, Kurt Hornik, 和 Achim Zeileis. 2004. 《kernlab: An S4 Package for Kernel Methods in R》. Journal of Statistical Software 11 (9): 1–20. https://doi.org/10.18637/jss.v011.i09.

Murphy, Kevin P. 2022. Probabilistic Machine Learning: An introduction. Cambridge, Massachusetts: MIT Press. https://probml.github.io/pml-book/book1.html.